Aproximar fracciones al número PI
Fracciones de enteros buscando el número π. Lenguaje ensamblador
Recuerdo que cuando yo tenía unos 14 años, mi profesor de matemáticas comentó que aun siendo π un número irracional, a lo largo de la historia muchas personas intentaron aproximarse a este valor de π mediante fracciones de números enteros. Por ejemplo, la fracción 22/7 da un resultado de 3,1428, que es un valor donde coinciden los 2 primeros decimales. Hay muchas curiosidades sobre el número π, por ejemplo, la anterior fracción 22/7 es conocida como el día de Pi, siendo este el 22 de julio. Hay muchísimas más curiosidades, hoy te voy a mostrar a encontrar fracciones de números enteros que se aproximen a este valor de π: ¿Cuál es la fracción de 2, 3, 4 o más dígitos que más se acerca al número π? Podría hacerlo con distintos lenguajes de programación pero hoy voy a hacerlo con el lenguaje que más rápido maneja el procesador: código máquina ensamblado directamente de lenguaje ensamblador.
Echando un vistazo a Wikipedia y a otras búsquedas en algunos apuntes y en la red, las fracciones de números enteros más conocidas son las siguientes:
- Alrededor del año 1650 a. C, el escriba egipcio Papiro de Ahmes calcula el valor de π como: 28/34 ~ 3,1605
- Sobre el año 1600 a. C, Tablilla de Susa (Babilonia): 25/8 = 3,125
- Arquímedes de Siracusa (287-212 a.C.) lo calcula entre
223/71 y 220/70
- Alrededor del año 20 d. C., el arquitecto e ingeniero romano
Vitruvio calcula π como el valor fraccionario 25/8
- En el siglo II, Claudio Ptolomeo proporciona el siguiente valor fraccionario: 377/120
- El astrónomo Wang Fang lo estimó en 142/45
- A finales del siglo V, el matemático y astrónomo chino Zu Chongzhi calculó el valor de π en 3,1415926 al que llamó «valor por defecto» y 3,1415927 «valor por exceso», y dio dos aproximaciones racionales de π: 22/7 y 355/113 muy conocidas ambas.
En mi juventud con 14 años, algunas veces pasaba el rato tomando una serie de decimales del número π y dividiendo por 10x intentaba encontrar la menor fracción posible. Por ejemplo:
Sin embargo, este proceso era muy lento y el número 31415926... al descomponerlo daba casi siempre números primos muy elevados, con lo cual llegaba un momento en el que no puedes continuar. Entonces, y aprovechando el procesador, se me ocurre que podemos ir haciendo las divisiones una a una y observar cuándo el resultado se aproxima a π
Para esto voy a crear una simple rutina en ensamblador, ya que este lenguaje lo ensamblaremos directamente en código máquina y es el más rápido con el que el procesador puede trabajar, además cuando se haga divisiones con varios decimales, se necesitará principalmente velocidad.
Hacer este ejercício que me he propuesto en ensamblador (procesador x86) es muy interesante ya que hay que trabajar con la Unidad de Punto Flotante (FPU) y normalmente un programador que lo haga en un lenguaje de alto nivel, no presta atención a esto ya que es el compilador el que se encarga de "traducirlo".
Código ensamblador
Sé que este código se puede optimizar mucho más (más rápido) ya que hacer divisiones cuando el divisor es mayor que el dividendo es una pérdida de tiempo, pero no lo voy a modificar (que es muy sencillo) porque quiero mostrar la rutina lo más clara posible. Si alguien está interesado en optimizar el código que lo comente...
0030BFC3 > $ 68 A0C03000 push 30C0A0 0030BFC8 . B9 E7030000 mov ecx,3E7 ; 999 dec 0030BFCD $ 68 6F12033A push 3A03126F 0030BFD2 . D90424 fld dword ptr ss:[esp] 0030BFD5 . 83C4 04 add esp,4 0030BFD8 . D9EB fldpi 0030BFDA . BB E8030000 mov ebx,3E8 ; 1000 dec 0030BFDF > > 4B dec ebx 0030BFE0 > > 53 push ebx 0030BFE1 . DF0424 fild word ptr ss:[esp] 0030BFE4 . 51 push ecx 0030BFE5 . DA3424 fidiv dword ptr ss:[esp] 0030BFE8 . 83C4 04 add esp,4 0030BFEB . D8E1 fsub st,st(1) 0030BFED . D9E1 fabs 0030BFEF . D8D2 fcom st(2) 0030BFF1 . DFE0 fstsw ax 0030BFF3 . 9E sahf 0030BFF4 . 0F86 1C000000 jbe 0030C016 ; pi.encontrado 0030BFFA > > 3E:D91C24 fstp dword ptr ds:[esp] 0030BFFE . 83C4 04 add esp,4 0030C001 .^ E2 DD l o o p d short 0030BFE0 ; pi.bucle2 0030C003 . B9 E7030000 mov ecx,3E7 0030C008 . 83FB 01 cmp ebx,1 0030C00B . 0F86 1D000000 jbe 0030C02E ; pi.fin 0030C011 .^ E9 C9FFFFFF jmp 0030BFDF ; pi.bucle1 0030C016 > > 8B4424 04 mov eax,dword ptr ss:[esp+4] ; ENCONTRADO 0030C01A . 8918 mov dword ptr ds:[eax],ebx 0030C01C . 834424 04 04 add dword ptr ss:[esp+4],4 0030C021 . 8948 04 mov dword ptr ds:[eax+4],ecx 0030C024 . 834424 04 04 add dword ptr ss:[esp+4],4 0030C029 .^ E9 CCFFFFFF jmp 0030BFFA ; pi.busca_siguiente 0030C02E > > 90 nop ; HA LLEGADO AL FINAL
Te pongo el mismo código tal cual lo he programado:
<$pi.4BFC3> ;Inicializa variables ;3A03126F = 0.0005 push $pi.4C0A0 mov ecx, 3E7 ; 999 dec push 3A03126F fld [esp] add esp,4 fldpi mov ebx, 3E8 ; 1000 dec @bucle1: dec ebx @bucle2: push ebx fild [esp] push ecx fidiv [esp] add esp,4 fsub st,st(1) fabs fcom st(2) fstsw ax sahf jbe @encontrado @busca_siguiente: fstp dword ptr ds:[esp] add esp,4 l o o p @bucle2 mov ecx, 3E7 cmp ebx, 1 jbe @fin jmp @bucle1 @encontrado: mov eax, [esp+4] ; ENCONTRADO mov dword ptr ds:[eax], ebx add dword [esp+4], 4 mov dword ptr ds:[eax+4], ecx add dword [esp+4], 4 jmp @busca_siguiente @fin: nop; HA LLEGADO AL FINAL
Explicación del código
El código es muy sencillo, pero hay que entender la Unidad de Punto Flotante. Lo que hace este código es generar 2 contadores: dividendo y divisor, números enteros desde el valor 1 hasta el 1000 (3E8hex). El registro ecx es el divisor y el registro edx es el dividendo. La primera instrucción push 30C0A0 guarda en la pila este valor que es la dirección donde se escribirán todos los datos encontrados. La instrucción push 3A03126F pasa posteriormente a la pila de punto flotante convirtiéndose en 0,0005 en la siguiente instrucción fld, y es el margen que voy a poner para que escriba los valores. fldpi carga en la pila de la Unidad de Punto Flotante el número π y es el que se va a utilizar para la resta.
Lo mejor para que veas lo que hace el código es que lo depures con un debugger como OllyDBG.
Viendo resultados
El ejemplo del código anterior tiene un dividendo y divisor máximos de valor 1000 y la precisión es de 0,0005. Tú puedes modificar ambos valores, por ejemplo, estas precisiones:
3556BF95 = 8e-07
33263D7C = 3.8e-08
34CFCCDB = 3.87e-07
3681E009 = 3.8e-06
3822580B = 0.000005
370637BD = 0.0000089
3851B717 = 0.00005
3A03126F = 0.0005
3BA3D70A = 0.005
Me dirijo en el código anterior a la dirección 0030C0A0, pongo un Breakpoint en 0030C02E y lo ejecuto. El resultado es el siguiente:
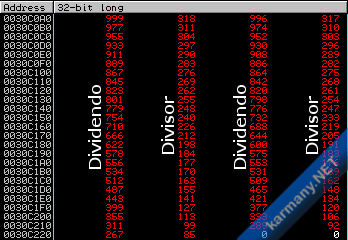
Como puedes ver, con una precisión en la resta de 0,0005, hay todavía muchos resultados. En la imagen anterior he resaltado el dividendo y divisor y la fracción más pequeña encontrada es: 267/85 ~ 3,1411764
Voy a indicarle más precisión en el resultado. Ahora le pongo: 0,0000089 y ejecutándolo solo me arroja 2 datos: 355/113 y 710/226. Esto significa que estas dos, son las fracciones de 3 cifras que más se aproximan al número π.
Finalizando
Ciertamente estas fracciones hubiesen sido imposibles de encontrar manualmente por el modo de ir reduciendo fracciones, pero para eso nos valemos hoy día del procesador... Como he dicho antes, el código se puede optimizar para que vaya más rápido (por ejemplo si quieres tener más precisión y mayor número de decimales) pero hubiese perdido la esencia de este tutorial. Tampoco he creado el código restante, por ejemplo, para mostrar una interfaz, botones... por lo mismo, aunque hacer esto último es muy sencillo. Creo que el código es muy interesante para trabajar con la Unidad de Punto Flotante sobre todo echa un vistazo a cómo se obtiene el flag de una operación de punto flotante, que veremos en otros tutoriales.




521030 / 165849 = 3.1415926535583573731003070861333981156
833719 / 265381 = 3.1415926535810778652546559897018596530
va casi 1500000 de verificaciones y nada aun
el ultimo es mas acertado
IMPRESIONANTE!!!! Excelente trabajo.
1980127 / 630294 = 3.1415926535870 561941976575326 407328248
¿Qué método has usado para encontrar estas divisiones?
salir = 'n'
while salir == 'n'
dividendo(enter o) + 1 = x
x / 2.5 = divisor (entero)
afuera = 'n'
while afuera == 'n'
dividendo / divisor = Y
si PI > Y
si división ultima es mejor a la anterior
guardar en sql
divisor -1
en caso contrario
si PI = Y
división exacta
reportarlo en sql
afuera = 's'
salir = 's'
en caso contrario
afuera = 's'
Lleva 2600000
1. 3 +?2/10 + (?2/2 +1)/10^4 + (?3/2 +5)/10^7 + ((??2 + 6) +7/10^3)/10^11 = 3,1415926535897 9
2. (7 +1/10) / ((9 + 4/100)/4) - ((8/?2) - 3) + 1/100)/10^7) - 1/(?1,25 + ?0,5 + ?2 + ?3 + ?5 + ?7 + ?8)*10^10 + (?3/2)/10^14 = 3,1415926535897 9
3. 6*((?1,25 +1,5)/5) - (2 + ?8)/10^5) + (4/?7)/10^7 + 1/ (??8 +10)*10^10
4. + 1 / (?1,25 - 4/1000)/10^10 = 3,14159265358978
5. 4*(0,5 + ((?0,5 +5)/10)/2) + ((2 + ?0,5) + 1)/10 + (1 / (?7/10)) /10^4 + (?5/10 + ?2)/10^6 + (2/?7)/10^10 + ((8 + ?7) - 0,5)/10^12 = 3,1415926535897 9
6. ?8 + 0,25 + 0,0625 + (1 /(150 + ((?7 + 3)/10) + 2)/10)*10) + 1 / (?0,5/3)*10^11
7. + 1 /(7 + ?5) / ?7)*10^12 = 3,1415926535897 9
Le he puesto a la resta una precisión de 2 e-07.
El resultado son estas fracciones:
9940/3164, 9585/3051, 9230/2938, 8875/2825, 8520/2712, 8165/2599, 7810/2486, 7455/2373, 7100/2260, 6745/2147, 6390/2034, 6035/1921, 5680/1808, 5325/1695, 4970/1582, 4615/1469, 4260/1356, 3905/1243, 3550/1130, 3195/1017, 2840/904, 2485/791, 2130/678, 1775/565, 1420/452, 1065/339, 710/226, 355/133
Observa que algunas son reducidas (710/226 = 355/133, 9230/2938 = 4615/1469).
2C0000 + 4C0A0 = 30C0A0 que es la dirección de la última imagen de este tutorial.